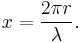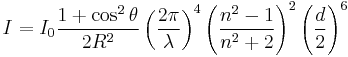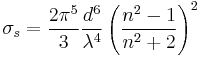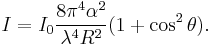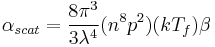Rayleigh scattering
Rayleigh scattering, named after the British physicist Lord Rayleigh, is the elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the light. The particles may be individual atoms or molecules. It can occur when light travels through transparent solids and liquids, but is most prominently seen in gases. Rayleigh scattering is a function of the electric polarizability of the particles.
Rayleigh scattering of sunlight in the atmosphere causes diffuse sky radiation, which is the reason for the blue color of the sky and the yellow tone of the sun itself.
Scattering by particles similar to or larger than the wavelength of light is typically treated by the Mie theory, the discrete dipole approximation and other computational techniques. Rayleigh scattering applies to particles that are small with respect to wavelengths of light, and that are optically "soft" (i.e. with a refractive index close to 1). On the other hand, Anomalous Diffraction Theory applies to optically soft but larger particles.
Contents |
Small size parameter approximation
The size of a scattering particle is parameterized by the ratio x of its characteristic dimension r and wavelength λ:
Rayleigh scattering can be defined as scattering in the small size parameter regime x ≪ 1. Scattering from larger spherical particles is explained by the Mie theory for an arbitrary size parameter x. For small x the Mie theory reduces to the Rayleigh approximation.
The amount of Rayleigh scattering that occurs for a beam of light depends upon the size of the particles and the wavelength of the light. Specifically, the intensity of the scattered light varies as the sixth power of the particle size, and varies inversely with the fourth power of the wavelength[1] .
The intensity I of light scattered by a single small particle from a beam of unpolarized light of wavelength λ and intensity I0 is given by:
where R is the distance to the particle, θ is the scattering angle, n is the refractive index of the particle, and d is the diameter of the particle.
The Rayleigh scattering coefficient for a group of scattering particles is the number of particles per unit volume N times the cross-section. As with all wave effects, for incoherent scattering the scattered powers add arithmetically, while for coherent scattering, such as if the particles are very near each other, the fields add arithmetically and the sum must be squared to obtain the total scattered power.
From molecules
Rayleigh scattering also occurs from individual molecules. Here the scattering is due to the molecular polarizability α, which describes how much the electrical charges on the molecule will move in an electric field. In this case, the Rayleigh scattering intensity for a single particle is given by[2]
The amount of Rayleigh scattering from a single particle can also be expressed as a cross section σ. For example, the major constituent of the atmosphere, nitrogen, has a Rayleigh cross section of 5.1×10−31 m2 at a wavelength of 532 nm (green light).[3] This means that at atmospheric pressure, about a fraction 10−5 of light will be scattered for every meter of travel.
The strong wavelength dependence of the scattering (~λ−4) means that shorter (blue) wavelengths are scattered more strongly than longer (red) wavelengths. This results in the indirect blue light coming from all regions of the sky. Rayleigh scattering is a good approximation of the manner in which light scattering occurs within various media for which scattering particles have a small size parameter.
Reason for the blue color of the sky
A portion of the light coming from the sun scatters off molecules and other small particles in the atmosphere. It is this scattered light that gives the sky its brightness and its color. As previously explained, Rayleigh scattering is inversely proportional to the fourth power of wavelength, so that shorter wavelength violet and blue light will scatter more than the longer wavelengths (yellow and especially red light). The resulting color, which appears like a pale blue, actually is a "weighted average" of all the scattered colors, mainly blue and green. Violet, though strongly scattered, is a minor component of the solar spectrum and is less efficiently detected by the human eye. Conversely, glancing toward the sun, the colors that were not scattered away—-the longer wavelengths such as red and yellow light—-are directly visible, giving the sun itself a slightly yellowish hue. Viewed from outer space, however, the sky is black and the sun is white.
The reddening of sunlight is intensified when the sun is near the horizon, because the volume of air through which sunlight must pass is significantly greater than when the sun is high in the sky. The Rayleigh scattering effect is therefore increased, removing virtually all blue light from the direct path to the observer. The remaining unscattered light is mostly of a longer wavelength, and therefore appears to be orange.
Rayleigh scattering primarily occurs through light's interaction with air molecules. Or, from a purely "optical", macroscopic point of view, blue sky comes from microscopic density fluctuations, resulting from the random motion of molecules composing the air. A region of higher or lower density has a slightly different refractive index than the surrounding medium, and therefore it acts like a short-lived particle that can scatter light in random directions. Smaller regions fluctuate more than larger ones, and, since short wavelengths are "disturbed" by small regions more than longer wavelengths, they are scattered more.
Some of the scattering can also be from sulfate particles. For years after large Plinian eruptions, the blue cast of the sky is notably brightened due to the persistent sulfate load of the stratospheric gases.
In locations with little light pollution, the moonlit night sky is also blue, because moonlight is reflected sunlight, with a slightly lower color temperature due to the brownish color of the moon. The moonlit sky is not perceived as blue, however, because at low light levels human vision comes mainly from rod cells that do not produce any color perception.
In optical fibers
Rayleigh scattering is an important component of the scattering of optical signals in optical fibers. Silica fibers are disordered materials, thus their density varies, on a microscopic scale. The density fluctuations give rise to energy loss due to the scattered light, with the following coefficient[4]:
where n is the refraction index,  is the photoelastic coefficient of the glass,
is the photoelastic coefficient of the glass,  is Boltzmann constant, and
is Boltzmann constant, and  is the isothermal compressibility. Tf is a fictive temperature, representing the temperature at which the density fluctuations are "frozen" in the material.
is the isothermal compressibility. Tf is a fictive temperature, representing the temperature at which the density fluctuations are "frozen" in the material.
In porous materials
λ−4 Rayleigh-type scattering can also be exhibited by porous materials. An example is the strong optical scattering by nanoporous materials.[6] The strong contrast in refractive index between pores and solid parts of sintered alumina results in very strong scattering, with light completely changing direction each 5 micrometers on average. The λ−4-type scattering is caused by the nanoporous structure (a narrow pore size distribution around ~70 nm) obtained by sintering monodispersive alumina powder.
See also
- Rayleigh Sky Model
- Rayleigh fading
- Ricean fading
- Raman scattering
- Optical phenomenon
- Dynamic light scattering
- Tyndall effect
- Critical opalescence
- Marian Smoluchowski
- Rayleigh Criterion
- Aerial perspective
References
- ^ Barnett, C.E. (1942). "Some application of wavelength turbidimetry in the infrared". J.Phys.Chem 46 (1): 69-75.
- ^ Rayleigh scattering at Hyperphysics
- ^ Maarten Sneep and Wim Ubachs, Direct measurement of the Rayleigh scattering cross section in various gases. Journal of Quantitative Spectroscopy and Radiative Transfer, 92, 293 (2005).
- ^ K.Rajagopal, Textbook on Engineering Physics, PHI, New Dehli 2008, part I, Chapt. 3
- ^ http://www.webexhibits.org/causesofcolor/14B.html
- ^ T. Svensson & Z. Shen, "Laser spectroscopy of gas confined in nanoporous materials", Applied Physics Letters 96, 021107 (2010). [1]
- C.F. Bohren, D. Huffman, Absorption and scattering of light by small particles, John Wiley, New York 1983. Contains a good description of the asymptotic behavior of Mie theory for small size parameter (Rayleigh approximation).
- Ditchburn, R.W. (1963). Light (2nd ed.). London: Blackie & Sons. pp. 582–585. ISBN 0122181018.
- Chakraborti, Sayan (September 2007). "Verification of the Rayleigh scattering cross section". American Journal of Physics 75 (9): 824−826. arXiv:physics/0702101. Bibcode 2007AmJPh..75..824C. doi:10.1119/1.2752825.
- Ahrens, C. Donald (1994). Meteorology Today: an introduction to weather, climate, and the environment (5th ed.). St. Paul MN: West Publishing Company. pp. 88–89. ISBN 0314027793.
Further reading
- Pedro Lilienfeld, "A Blue Sky History." (2004). Optics and Photonics News. Vol. 15, Issue 6, pp. 32–39. doi:10.1364/OPN.15.6.000032. Gives a brief history of theories of why the sky is blue leading up to Rayleigh's discovery, and a brief description of Rayleigh scattering.